An idea
Could one use unsupervised reinforcement learning to fly an aircraft?
Digging deeper
To start, we need a flight simulator. Flight simulators have been around for ages and we could use any of them by just reading the screen and inputting commands, but this task would be way too complex to tackle using only vision. Aircraft are machines that require a machine-to-machine interface for control and state monitoring, a simulator with an API is essential to retrieve data from the simulation (such as aircraft position, speed, etc.) and to send control commands (like pitch, yaw, speed, etc.). While popular flight simulators like MSFS and X-Plane offer SDKs, these are better suited for extending the game experience rather than fully controlling it through scripts.
I finally settled on an open-source flight simulator called Flightgear, which also runs on Linux. Flightgear has a nice API that you can control with HTTP, Telnet, and its own sockets-based protocol. These are abstracted in the Flightgear Python package. Running unsupervised learning requires thousands and thousands of training runs and after a few trials using the Python package, I realized that the flight simulator itself is not that fast to set up due to the loading of UI resources such as weather, the aircraft model, scenery, etc.
I then realized there is no need for the full simulator. We just need the flight dynamics model. As the Flightgear wiki puts it, "A Flight Dynamics Model (FDM) is a set of math equations used to calculate the physical forces acting on a simulated aircraft, such as thrust, lift, and drag." The default FDM for Flightgear is JSBSim.
Luckily, there is a relatively well-maintained gym environment already for JSBSim called jsbgym. This finally puts us in a situation where we are able to run reinforcement learning techniques on the problem.
The solution
Now that we have the Gym, we just need a proper reinforcement learning algorithm to create a model.
Our chosen Gym includes two tasks
- HeadingControlTask: "A task in which the agent must perform steady, level flight maintaining its initial heading."
- TurnHeadingControlTask: "A task in which the agent must make a turn from a random initial heading, and fly level to a random target heading."
JSBGym was developed by Gordon Rennie for their MSc dissertation. Although neither training data nor trained models are available, we know that the author used Proximal Policy Optimization (PPO) algorithm to achieve their results.
We first set out to replicate what we know about the results.
Reproducing the results
For PPO implementation, we will use CleanRL's PPO continuous action variant which is a nice one-file implementation of the algorithm. We also load JSBGym locally to be able to modify the tasks separately.
Before getting into the training and evaluation, I wanted to make sure I can save the trained model and separately evaluate the results if needed.
This proved more difficult that I expected.
Having little prior experience from Deep RL I expected to be able to save the model using:
torch.save(agen.state_dict(), f"models/{run_name}/agent.py")
However, as I found out, we need to save observations as well which, plugged straight into the code turned out to be rather wacky:
# ppo_continuous_action.py
f = open(f"models/{run_name}/obs.pickle", "wb")
pickle.dump(envs.envs[0].env.env.obs_rms)
# eval.py
# overwrite the observations after loading ht emodel
envs.envs[0].env.env.obs_rm = pickle.load(f)
With this, we get expected results.
The most noticeable feature of the resulting model is its rapid adjustment of the control surfaces. The rudder and ailerons continuously shift from left to right, while the elevator moves up and down in quick succession. These actions occur at a high frequency, creating fluctuations at every step. Despite the seemingly opposing control movements, they effectively balance each other out, allowing the model to maintain the aircraft close to the target altitude and heading—achieving the original goal of the task.
Can the rough controls be improved? The model currently has unrestricted access to adjust the control surfaces from one extreme to the other. However, it predominantly selects actions at either extreme, which is not how a pilot would typically operate an aircraft. In real-life scenarios, extreme inputs often lead to excessive responses, which are undesirable. For example, when driving a car, the driver doesn’t turn the steering wheel all the way to the left to make a left turn. Instead, they adjust the wheel smoothly and gradually until the car is oriented as desired. Extending this analogy to an aircraft, the challenge is even greater. Pilots must consider the structural stress caused by forces acting in three dimensions. Excessive inputs can generate forces that exceed the aircraft's structural limits, potentially causing damage.
Fixing the jerky movements
Instead of giving the model unrestricted access to the control surfaces, we could emulate how a human pilot flies an airplane by ensuring smoother adjustments at each step. For instance, if the model commands a full left turn while the airplane is banking to the right, we could gradually adjust the wings to turn slightly left. If the model continues to command a left turn in subsequent steps, the wings would incrementally turn further left. This approach gives the model more time to observe the state of the aircraft after each action. It might eventually find the plane flying level and decide that no further adjustment is necessary.
In JSBSim, control surfaces are set using values ranging from -1 to 1. For the ailerons, -1 represents at full left position, 1 represents a full right position, and 0 indicates level ailerons.
To implement smoother transitions, we start by limiting the adjustments to an eighth of the maximum action. For example, if the model commands a value of -1 while the ailerons are currently at 1, we would first set the ailerons to 0.75, then to 0.5, 0.25, and so on. Small adjustments by the model, such as those within 0.25, are left unmodified, as they are considered acceptable.
The original task includes the rudder as one of the control actions. However, in practice, the rudder is not essential for maintaining level flight. Rudder is applied only slightly during turns to ensure a "clean" turn; without it, the turn may result in suboptimal flying. The original author attempted to address this by introducing additional rewards, which rewarded the model for minimizing the aircraft's sideslip angle and ensuring the wings are level. Unfortunately, this approach did not yield successful results. Since I am unsure how to model the rudder's use more effectively, I will completely disable the rudder action in my implementation and observe the outcomes.
This seems to have worked suprisingly well!
Analysing the results
How can we evaluate how well the model performed? There are several potential ways to measure the "jerkiness" of a model's actions. Ultimately, I decided to log the following objective metrics from the training runs:
- Maximum load factor: The highest stress experienced by the aircraft during the run (values closer to 1 indicate better performance).
- Mean track error: The average deviation from the intended course during the run (smaller values are preferable).
- Mean altitude error: The average deviation from the target altitude during the run (smaller values are better).
The maximum load factor provides insight into how much stress was applied to the aircraft and whether the model operated as intended. While we could also measure an average load factor, the maximum value is more informative in this context. As noted in Wikipedia, standard airplanes, such as the Cessna C172 used in this simulation, are designed to handle load factors ranging from −1.52g to +3.8g. The maximum load factor is therefore a critical metric for assessing whether the flight behavior remains within "normal" operating conditions. Unlike an average load factor, the maximum ensures that stress levels exceeding these limits even briefly, are captured.
I initially chose to smooth the action by 1/8th of the model's input arbitrarily. To explore more effective approaches, I developed additional methods for smoothing the control actions:
- Non-linear actions: Adjustments closer to the current state are made more gradually, while larger deviations are smoothed less aggressively.
- 1/20th action: Instead of adjusting the controls by 0.25 (1/8th), the changes are limited to 0.1 per step.
Training models using these methods produced the following results:
To explain this:
- All models, except the one with non-linear smoothing controls, achieve good results relatively quickly, as shown by the Mean track error.
- The original task achieves the worst (i.e., highest) Maximum load factor, while the other models yield similar results around ~2.5g.
- All models perform well in maintaining altitude. However, for reasons unknown, all models show an increase in altitude error toward the end of the training episodes. After analyzing the data, I found that this error is mostly positive, meaning the models tend to fly slightly higher than the target altitude. The exact cause remains unclear, but it could be due to the aircraft’s instability, with only the gentlest control actions (20th) effectively keeping the plane at the target altitude.
- The rewards are based on proximity to the target altitude and track heading. Smoothing 8th slightly lags behind the Original task in rewards towards the end of the training, likely due to slightly poorer performance on maintaining the altitude.
As observed, none of the alternative approaches performed as well as the originally chosen approach. What a luck!
Therefore, I'll consider the Smoothing 8th model as "good enough" for now.
Extending the environment
Initially, I experimented with adding tasks like changing altitude and maintaining a steady vertical speed. However, these tasks didn’t yield good results, as it became clear that achieving success would require significantly restricting the model’s behavior.
For example, I implemented a task to ascend to a set altitude. At first, this seemed promising, but I soon discovered that the model repeatedly failed by pitching the nose up to gain altitude. Over time, the aircraft began to stall due to a loss of speed. A more refined approach would be to maintain a steady vertical speed until the aircraft reaches the target altitude. However, in the end, this task proved very similar to what is required for level-flight tasks.
Beyond the prototype
In reality, using reinforcement learning for controlling an aircraft is likely not a good solution at this point. Autopilots have been successfully used in aircraft since World War II, and it would be difficult to argue that reinforcement learning techniques could improve upon current systems, especially in safety-critical applications like air travel.
A simple and effective autopilot implementation is the Proportional–Integral–Derivative (PID) controller, whose mathematical foundations date back to the 1800s.
Here’s a good example of a FlightGear autopilot controlling trim (keeping the plane level) in response to changes in vertical speed using a PID controller:
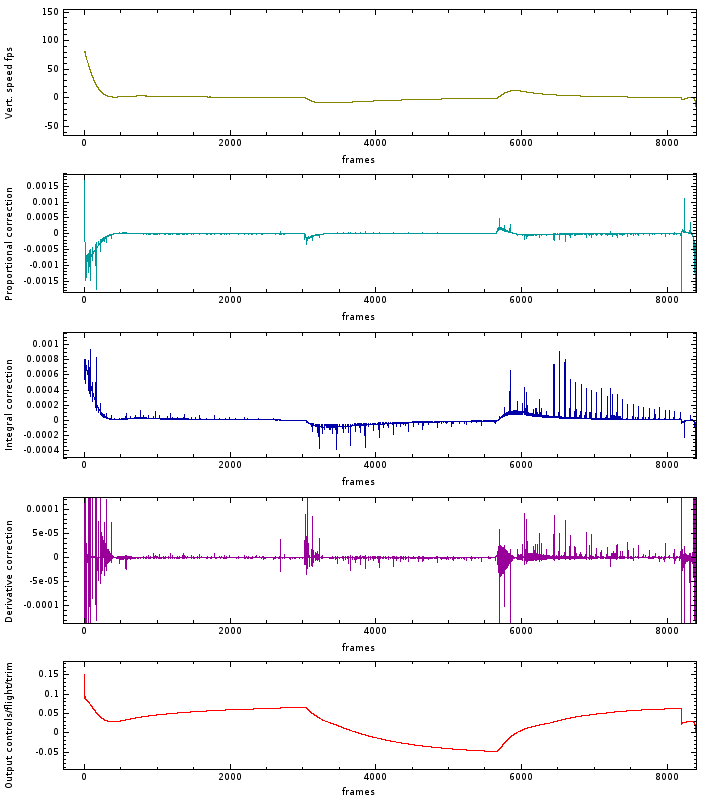
In this system, the aircraft’s vertical speed is used as an input for the three PID components (P, I, and D). The sum of these components is then used to adjust the trim.
Each component of the PID controller contains a K variable, which must be adjusted to fine-tune the system’s performance. In aircraft, vertical speed is measured by changes in static pressure, and it takes some time to settle after the aircraft has stopped climbing or descending. The vertical speed doesn’t need to be zero constantly, as changes in air pressure, wind, and other factors can influence the readings. The K variable allows for adjustment in the system’s response to these changes.
The following GIF shows how the system responds to changes with different K values:
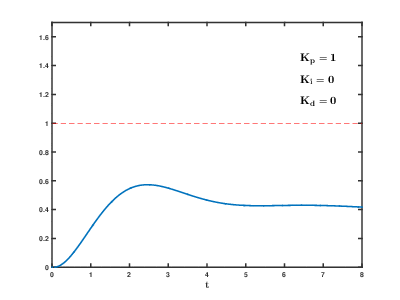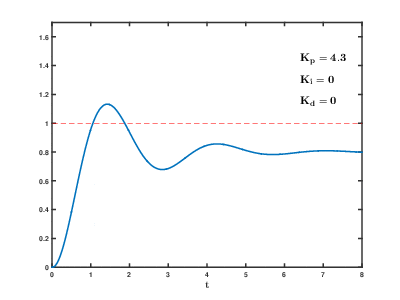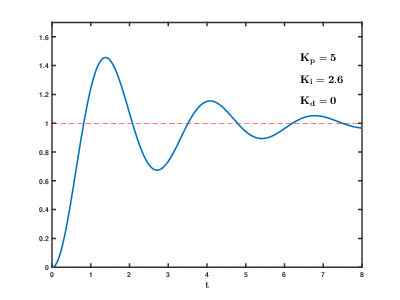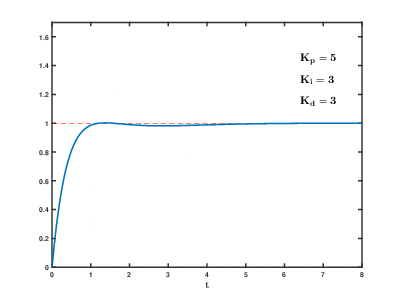
Implementing a traditional autopilot is left as an exercise for the reader. :)
Markus